Introducción
La producción de carne a nivel mundial se quintuplicó entre 1960 y 2017, hasta alcanzar 330 millones de toneladas en peso de canal (FAO, 2016). Para el 2018 se incrementó a 342 millones de toneladas y en el 2019 se presentó una disminución de 2,6%, afectada por la reducción en la producción de carne de cerdo en Asia y bovina en Estados Unidos y Australia (FAO, 2020). Las proyecciones para el período 2020-2021 prolongaban la tendencia a la baja con una reducción de 1,7% con respecto al 2019, que pudo agravarse por los efectos negativos de la pandemia mundial por COVID-19 (FAO, 2020).
La pandemia ha generado un escenario de incertidumbre para las proyecciones en el mercado de alimentos. Con respecto al consumo per cápita mundial de carne de res, se estima un incremento anual de 5% en el período 2019-2029, con una mayor participación de los países en vías de desarrollo en la demanda, por el crecimiento de la población y el ingreso promedio (Ritchie, 2019). Se espera que los gustos y preferencias de consumo, y la percepción hacia los efectos secundarios de sistemas productivos sobre el ambiente y de bienestar animal en el comercio mundial, marquen las proyecciones del sector agrícola en los próximos diez años (OCDE y FAO, 2020).
En Costa Rica, la carne bovina es una de las principales fuentes de proteína animal. En 2017 se registró una frecuencia de consumo de una y dos veces por semana en hogares costarricenses, con un promedio por hogar de 2,2 kg semanales; la provincia de Guanacaste encabezó la lista con 2,6 kg (CORFOGA, 2017). Mientras que la estimación de consumo aparente per cápita fue de 10,78 kg, con variaciones mínimas de 0,3% hasta el 2019 (CORFOGA, 2020). Estas condiciones de consumo recaen sobre los retos de producción de carne bovina en el país, la cual se basa principalmente en la alimentación con forrajes de pastoreo y rotación planificada.
El más reciente Censo Nacional Agropecuario registró cerca de 37 mil fincas de ganado vacuno en 2014, el mayor hato para producción de carne se concentraba en Guanacaste (INEC, 2015). Las fincas ganaderas se caracterizaban por una reducida extensión y baja densidad (cabezas de ganado por hectárea), el 43% tenían una extensión menor a 10 ha y el 81% menor a 50 ha, con un rango promedio de 20 a 30 ha (INEC, 2015).
La ganadería costarricense es extensiva y poco tecnificada, y resulta difícil migrar a sistemas estabulados de manera inmediata, ya que el costo de alimentación podría representar hasta el 80% de los costos productivos (Hernández et al., 2016). Ante este panorama, es necesario planificar y mejorar el manejo de las fincas ganaderas, especialmente en Guanacaste, si se desea aprovechar al máximo la incidencia de radiación solar sobre las pasturas y la disponibilidad del recurso hídrico que provee el Distrito de Riego Arenal Tempisque (DRAT).
La Programación Lineal (PL) se ha utilizado para planificar la producción, los niveles de ingresos y las interacciones económicas de diversos sistemas de producción bovina (Botero, 2003). Una de sus ventajas recae sobre la capacidad para evaluar diversos escenarios simulados con base en indicadores de rentabilidad (Holmann y Rivas, 2005).
En la producción de ganado de engorde existen factores que limitan y condicionan la etapa final de crecimiento de los animales, tales como la edad del destete, la raza, las condiciones ambientales y de manejo, pero el más relevante es la alimentación, de ahí la importancia de formular efectivamente la ración alimenticia (García et al., 1998). Una formulación inadecuada podría provocar pérdida de dinero en el sistema productivo, tanto por la subalimentación como por la sobrealimentación: primero porque se alarga el tiempo de estadía del bovino en el sistema y segundo porque se genera un desperdicio de alimentos.
Para solventar esta problemática, la PL facilita la formulación de raciones al mínimo costo, la optimización del ciclo productivo y la maximización de utilidades (Zgajnar et al., 2010). En Argentina se elaboró un modelo de optimización para el engorde de bovinos en pastoreo que priorizó el uso de suplementos en las primeras etapas de crecimiento debido a la mayor eficiencia de conversión, una reducción en el tiempo de finalización del novillo y un incremento en el margen bruto de ganancia (García et al., 1998).
También se ha evaluado la conveniencia de sustituir el grano de maíz por avena como suplemento en sistemas estabulados (De Gaetano, 2018). Esta investigación demostró el beneficio técnico y económico de sustituir los granos a diferentes niveles en la ración, aunque si el precio del maíz era menor, el modelo priorizaba su incorporación en la ración (De Gaetano, 2018). Por su parte, Soto y Reinoso (2012) abordaron la formulación de raciones al mínimo costo con restricciones sobre el consumo de materia seca y otros nutrientes suministrados en Uruguay, país que se ha caracterizado por su producción ganadera bajo sistemas de pastoreo.
La investigación de Widiati (2006) aportó un importante avance en la aplicación de PL, con la optimización de recursos en sistemas con múltiples actividades sujetos al incremento de la rentabilidad. Los resultados delimitan el área de terreno que se debe destinar para cada actividad productiva hasta alcanzar un aumento del 85% en la rentabilidad, que se vio beneficiada principalmente por la venta de novillos a su edad óptima (Widiati, 2006).
La programación lineal también ha sido aplicada en la producción de lácteos. En Perú se utilizó para optimizar las ganancias en la producción de leche de pequeños y medianos productores (Acero, 2017). También se implementó para medir la influencia de la maximización de la producción de derivados lácteos sobre la utilidad (De la Cruz, 2017), medir el impacto de los cambios tecnológicos sobre los resultados económicos de empresas lecheras (Ariza, 2020), caracterizar las interacciones que optimizan la producción lechera (Cursack et al., 2008) y determinar los efectos de la cadena de suministro sobre la producción bovina (Terán, 2015).
En vista de lo discutido hasta el momento, existe evidencia que respalda el uso de métodos cuantitativos para optimizar costos o utilidades en unidades de producción agropecuaria, sin embargo, la literatura disponible no ha logrado determinar un modelo de optimización de costos para la producción de ganado en Costa Rica. Por lo tanto, en este artículo se sugiere un modelo de optimización del costo de alimentación para engorde de ganado de carne a partir de una dieta a base de forrajes y otros suplementos en una finca ubicada en Cañas, Guanacaste.
Referente teórico
La PL es una herramienta de análisis cuantitativo y modelación matemática, que ayuda en la planeación y la toma de decisiones respecto a problemas básicos de la economía como la asignación eficiente de recursos (Render et al., 2012). Chase y Jacobs (2014) la describen como un conjunto de técnicas matemáticas para asignar, en forma óptima, los recursos limitados a distintas demandas de diferentes unidades que compiten por ellos. Para plantear un problema de optimización se deben cumplir una serie de condiciones básicas, a saber (Chase y Jacobs, 2014): a) tener recursos limitados; b) tener un objetivo explícito; c) debe existir linealidad entre los recursos y el producto final; d) debe existir homogeneidad; e) debe existir divisibilidad, ya que supone que los productos y recursos se pueden subdividir en fracciones.
Además de las condiciones descritas anteriormente, las variables de decisión no pueden ser negativas, los criterios para seleccionar los mejores valores de las variables de decisión pueden ser descritos como una función lineal y las reglas de funcionamiento del modelo pueden expresarse como un conjunto de igualdades o desigualdades lineales (Render et al., 2012).
En los modelos de PL se define una función objetivo, que representa aquello que se desea optimizar, sujeta a las variables de decisión, que no se conocen y quedan definidas para lograr la optimización (Izar, 1996). El modelo también incorpora restricciones que delimitan el problema, como la cantidad de materia prima para la formulación de una ración alimenticia, y restricciones implícitas, que son aquellas ocultas en el problema, pero que deben ser tomadas en cuenta en el planteamiento y la resolución, como la no negatividad (Izar, 1996).
Para resolver problemas de optimización, George Dantzing desarrolló el método simplex, que se caracteriza por su versatilidad y por permitir incorporar un elevado número de variables y restricciones (Izar, 1996). Este es un proceso matricial iterativo para manejar variables no negativas que toma como posible solución uno de los vértices partir del origen, es decir, en las siguientes iteraciones el simplex se mueve hacia otros vértices hasta encontrar el óptimo, que sucede cuando un vértice tiene mejor valor de la función objetivo que los dos vértices adyacentes próximos (Izar, 1996).
Metodología
El estudio de caso se ubica en Cañas de Guanacaste, en una finca de engorde de novillos vacunos con pastoreo racional distribuidos en 28 lotes. Cada lote tiene una extensión promedio de 3 100 m2 con pasto Mombaza (Panicum maximum), cercas eléctricas, sistema de riego por aspersión, fertirriego programado y manejo controlado de malezas, plagas y enfermedades. Para la fecha del estudio se contaba con 51 cabezas de ganado, principalmente de las razas Brangus, Brahman y Nelore, que pastoreaban cerca de 17 horas diarias, con refugio bajo sombra (en una extensión de 600 m2) en las horas de mayor radiación solar, y suministro de agua y alimento de acuerdo con los requerimientos nutricionales. Estas condiciones se implementaron para obtener la mayor ganancia diaria de peso (GDP) posible en los animales, ya que la calidad nutricional de las pasturas varía en las épocas lluviosa y seca.
Fuentes de información
Se utilizó información proveniente de los análisis bromatológicos de las pasturas, el precio de las materias primas en comercios aledaños a la finca y requerimientos nutricionales de los bovinos a diferentes pesos para alcanzar una determinada GDP. Se asumió con criterio de experto, que la empresa contaba con sistemas de planificación de actividades, registros suficientes de control y manejo estandarizado para minimizar las variaciones en la calidad de las pasturas según la época del año.
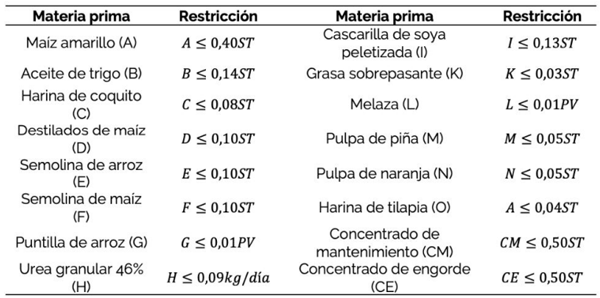
Con los resultados de los análisis bromatológicos se realizó una predicción del consumo de los nutrientes del pasto en novillos y toretes de engorde, que permitió determinar las materias primas necesarias para la suplementación en función del manejo alimenticio, el aporte nutricional y su disponibilidad. Dentro de las materias primas para la suplementación, se consideraron productos derivados de maíz, soya y arroz, acemite de trigo, pulpas de naranja y piña, harina de coquito, melaza, grasa sobrepasante, urea azufrada y harina de tilapia, minerales como calcio y fósforo vitaminado, fosfato monocálcico y algunos concentrados de engorde y mantenimiento preparados.
Para determinar los requerimientos nutricionales según peso vivo (PV) y GDP del animal, se utilizaron como base los componentes y cantidades estimadas por Cerdas-Ramírez (2013), además de su criterio de experto según la zona geográfica y la pastura implementada (R. Cerdas-Ramírez, comunicación personal, 2017). Cabe destacar que, la producción por pastoreo racional y el uso de una única especie forrajera, mejoran la precisión en las estimaciones de contenidos nutricionales de la base alimenticia para calcular la suplementación necesaria de los animales.
Los requerimientos nutricionales del ganado de engorde se basan en cuatro elementos fundamentales: el peso del animal al entrar al sistema de producción, la GDP objetivo, la condición fisiológica y el medio en que se desarrolla el bovino (temperatura, distribución de potreros, áreas sociales, bebederos y comederos) (R. Cerdas-Ramírez, comunicación personal, 2017).
Supuesto del modelo
El modelo de optimización cuantifica la combinación de materias primas de menor costo para alcanzar los requerimientos nutricionales del engorde de los semovientes bajo los siguientes supuestos:
a) El peso vivo de los animales varía en un rango de 200 a 450 kg con una GDP de 0,5 a 2 kg.
b) Los requerimientos nutricionales no consideraron condiciones de clima, distancias recorridas, tasa de bocado y cantidad de barro en las patas del animal.
c) Los animales consumen el 2% de la ración de materia seca en el tiempo de pastoreo, dada la calidad del pasto, el manejo rotacional y la selectividad natural de consumo.
d) La disponibilidad de cantidad y calidad del pasto está dada por un manejo agronómico estandarizado adecuado, así como el control de la carga animal.
e) El análisis bromatológico y los proximales de los alimentos cuentan con información fidedigna para el modelo.
f) El precio de venta de las materias primas incluye el transporte a la finca con un viaje semanal, una distancia de 4,5 km al centro de Cañas y un costo total de 14,16 USD.
Función objetivo
Es la combinación de los productos alimenticios que satisfacen los requerimientos nutricionales de los bovinos y cumplen con un mínimo costo por ración. La función que minimiza los costos es la siguiente:
Donde, Pi es el precio de cada materia prima incluida en el modelo y Qi la cantidad re-querida de cada materia prima.
Restricciones de la función objetivo
La función objetivo está sujeta a las siguientes restricciones nutricionales técnicas y de capacidad ruminal del bovino:
CUADRO 1. Restricciones nutricionales según peso vivo (PV) y ganancia diaria de peso (GDP)
El saldo de los requerimientos nutricionales lo constituyen las diferencias entre el aporte de la pastura y los requerimientos necesarios indicados por Cerdas-Ramírez (2013) para alcanzar la GDP según el peso promedio del animal.
CUADRO 2 Restricciones de capacidad ruminal del bovino según peso vivo (PV) y ganancia diaria de peso (GDP)
Las necesidades nutricionales de cada animal se deben satisfacer de acuerdo con una cantidad de materia seca y fibra cruda en la ración, definida por el peso vivo del animal.
CUADRO 3 Restricciones técnicas según peso vivo (PV) y suplementación total (ST)
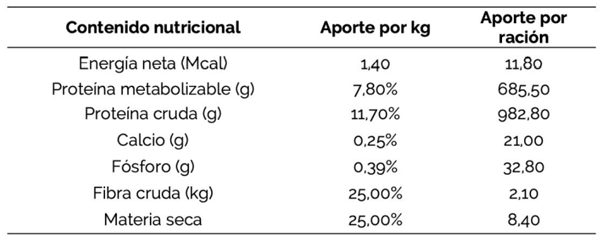
Para el total de materias primas que se incluyen en las restricciones del modelo de optimización, se consideraron 12 diferentes proveedores en las inmediaciones de la finca. También se tomó en cuenta el contenido nutricional del pasto Mombaza según los resultados de análisis bromatológicos de la pastura (Cuadro 4).
CUADRO 4 Contenido nutricional del pasto Mombaza y su participación en la ración total diaria
Variación en la ganancia operativa
Después de obtener la ración alimenticia al mínimo costo que satisface los requerimientos nutricionales de los animales, se realizó un análisis de la variación en la ganancia operativa total monetaria de la finca en un año calendario, para lo cual se asumió que:
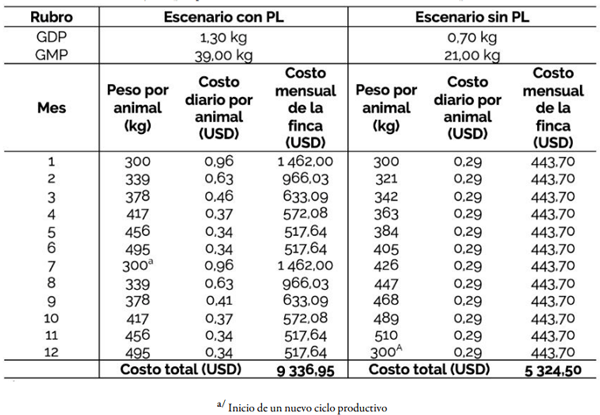
a) Se incorporan al sistema 51 animales cada ciclo productivo con un peso promedio de 300 kg en condiciones fisiológicas y genéticas adecuadas.
b) La ración alimenticia sin optimización es constante, con una GDP de 0,70 kg por animal (21 kg de ganancia mensual de peso (GMP)), al igual que el precio y las cantidades suplementadas.
c) La ración alimenticia optimizada varía en función de los requerimientos nutricionales con una GDP de 1,30 kg por animal (39 kg de GMP).
d) La calidad del pasto no cambia a lo largo del año.
e) El rango ideal de peso promedio de salida al mercado es de 495 kg a 510 kg por animal.
f) Los costos operativos de la empresa son constantes.
Resultados
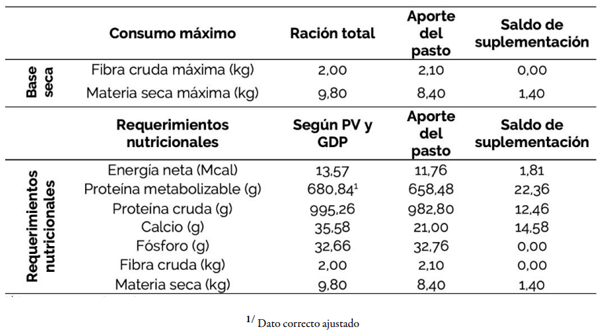
El modelo de optimización calculó el aporte del pasto para cada ración, una vez que se definió la capacidad de consumo máximo del animal en base seca según su PV. En este caso, el saldo que resulta de la diferencia entre la ración total y el aporte del pasto, es la cantidad de contenido nutricional faltante en la ración que se suplementará al mínimo costo, mientras que los componentes nutricionales se calcularon según el PV y la GDP estimadas (Cuadro 5).
CUADRO 5 Resultados de la programación lineal, saldo de suplementación diario según el aporte nutricional de la pastura
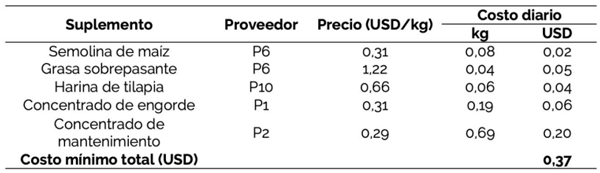
Los resultados de la optimización indican la cantidad, el tipo, el proveedor y el precio de los alimentos, que minimizan el costo de la ración que satisface los requerimientos nutricionales (Cuadro 6). De toda la variedad de materias primas consideradas, con sus condiciones nutricionales particulares y precio de venta, el modelo selecciona únicamente tres materias primas, un concentrado de engorde y uno de mantenimiento, que suplementan la ración balanceada para los animales con un costo mínimo de 0,37 USD diarios por animal y una GDP de 1,3 kg.
CUADRO 6 Resultado de la programación lineal y costos de la ración diaria por animal
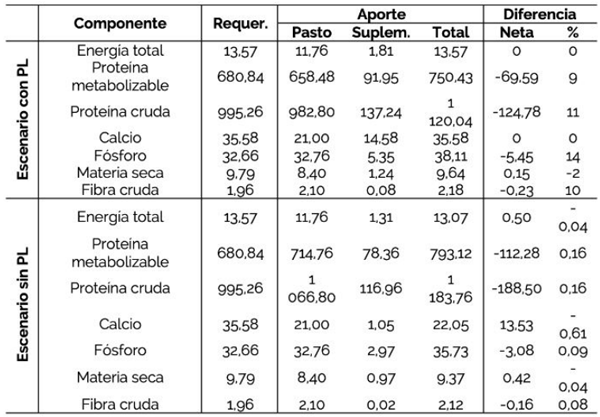
Para comprobar los requerimientos del modelo de optimización con el aporte total de la suplementación y el pasto, se analiza la diferencia de cada componente nutricional en la ración alimenticia total para un peso promedio de 420 kg por animal y una GDP de 1,3 kg (Cuadro 7). Los componentes que presentan una diferencia porcentual igual a cero cumplen efectivamente la condición, los que muestran una diferencia mayor que cero aportan más de lo requerido (superávit) y los que indican una diferencia menor que cero aportan menos de lo requerido (déficit).
Para demostrar la optimización se compararon los resultados con la suplementación alimenticia utilizada en la finca previo a esta investigación, misma que se basaba en el suministro de melaza, destilado de maíz, urea y otros minerales, con un costo diario de 0,29 USD por animal.
CUADRO 7 Comparación de requerimientos nutricionales en dos escenarios con y sin programación lineal (PL)
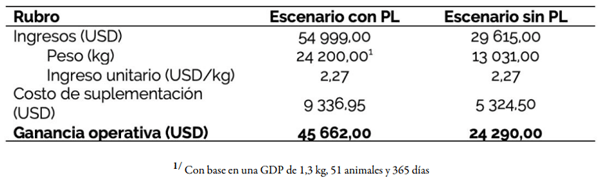
La ración alimenticia balanceada por animal en un escenario con optimización tiene un costo 27,59% mayor que la ración utilizada previamente, aunque la GDP es 85,71%. Comparativamente, el costo por kilogramo de GDP en el escenario sin PL es de 0,42 USD y con la implementación del modelo disminuye a 0,28 USD.
Variación en la ganancia operativa
Si en la finca se implementan el modelo de optimización sugerido, la empresa incurría en costos de suplementación 75% mayores que en un escenario sin modelación (Cuadro 8). Sin embargo, con el supuesto del rango de peso ideal promedio por animal de 495 kg a 510 kg como requisito para salir al mercado, en el escenario con PL se contaría con dos ciclos de producción de 51 cabezas de ganado por ciclo en un año calendario, es decir, el ganado permanecería en la finca 6 meses. Mientras que en el escenario sin PL el ciclo de producción tiene una extensión temporal de 11 meses.
CUADRO 8 Variación de los costos de suplementación en dos escenarios con y sin programación lineal (PL) a diferentes niveles de peso
Si se asume un precio de subasta de 2,27 USD/kg, el incremento en la ganancia operativa anual de la empresa es de 21 372 USD en el escenario con PL, es decir, 87,99% mayor (Cuadro 9). Además, se ofrece al consumidor una carne más saludable y de mayor calidad, debido a la salida de los animales al mercado con una menor edad en comparación con un escenario sin optimización.
CUADRO 9 Variación de la ganancia operativa anual en dos escenarios con y sin programación lineal (PL)
Discusión
En la finca se suplementaba una ración alimenticia desbalanceada debido al déficit de minerales. Además, la ración estaba compuesta por urea sin azufre. Estos componentes deben adicionarse en conjunto para lograr que las bacterias del rumen sinteticen los aminoácidos azufrados que facilitan la incorporación de proteínas al cuerpo (R. Cerdas-Ramírez, comunicación personal, 2017).
Con respecto a las condiciones de la capacidad ruminal del animal con la implementación del modelo de PL, las variaciones en la materia seca (aporte 2% menos de lo establecido) y la fibra cruda (aporte 10% más de lo establecido) son válidas, ya que el 15% de la variación puede ser compensada con la falta de certeza del consumo del 2% de materia seca de los animales en el potrero, y otros criterios no contemplados como la distancia de desplazamiento de los animales, las condiciones de estrés por el clima y el tamaño del bocado (Cerdas-Ramírez, 2013).
Implementar la ración balanceada sugerida reduciría el costo por kilogramo de GDP en un 33% aproximadamente, lo que podría traer mayores beneficios que el simple hecho de la reducción, pues los animales en engorde podrán alcanzar un peso meta determinado en un menor lapso de tiempo, que propicia su pronta salida al mercado y genera mayor flujo de efectivo para la empresa. La importancia del flujo de efectivo en una empresa agropecuaria radica en la disponibilidad monetaria, para cubrir los costos diarios de producción establecidos o que surjan en un momento determinado, y la disponibilidad de invertir según las condiciones de liquidez (Armijos, 2018).
Al igual que De Gaetano (2018), en esta investigación la programación lineal permitió la formulación de una ración balanceada en la que se prioriza la incorporación de ciertas materias primas sobre otras que, por lo general, aportan menores beneficios alimenticios o se encuentran en el mercado a un mayor precio. Esta investigación se enfocó en tres de las ventajas de la PL en sistemas productivos: 1) la asignación correcta de recursos, 2) el mínimo costo y 3) el incremento de la ganancia (García et al., 1998). Su efectividad podría generar otro tipo de beneficios como la mejora en la toma de decisiones operativas y administrativas de manera objetiva y respaldada en métodos cuantitativos.
Conclusiones
El modelo de optimización desarrollado a través del método de programación lineal que se sugiere en esta investigación, determinó la ración alimenticia balanceada que satisface los requerimientos nutricionales de los bovinos a un mínimo costo. Estos resultados son un respaldo cuantitativo de las decisiones operativas en la finca, que permitirá obtener la GDP definida con la disponibilidad de materias primas a diferentes precios en la zona de Guanacaste.
Una buena alimentación de los bovinos incluye una ración balanceada que promueve una GDP mayor, mejor calidad en la carne y disminuye el tiempo de permanencia de los animales en el sistema de producción, con ciclos productivos cortos que mejoran el flujo de efectivo del negocio según la variación en la ganancia operativa.
Debido a la importancia del costo de la alimentación en el ganado de engorde, el control de la suplementación es fundamental, tanto de la cantidad como de la calidad de los alimentos y el balance de la ración, pues suplementar sin balancear promueve el desperdicio de recursos y de tiempo, que afectan directamente la rentabilidad de la finca.
El modelo de optimización estimó los resultados con base en la realidad de las condiciones nutricionales de las pasturas de la finca y la disponibilidad de fuentes alimenticias. Inclusive, podrían fomentarse sistemas de economía circular que incorporen a la alimentación ensilajes, pacas de heno u otros productos secundarios originados en la misma finca, para fortalecer los niveles de eficiencia y de competitividad.
Para mejorar la rentabilidad de las empresas agropecuarias es recomendable utilizar herramientas efectivas de análisis cuantitativo como la programación lineal que permitan optimizar los costos de producción, tal y como se demostró en esta investigación.
Agradecimientos
Se agradece a la Vicerrectoría de Investigación de la Universidad de Costa Rica por el apoyo financiero para esta investigación mediante el proyecto inscrito B05A12 denominado "Modelación econométrica de mercados agrícolas y aplicación de métodos cuantitativos para optimización de procesos en agronegocios". Asimismo, se agradece al Programa de Posgrado en Gerencia Agroempresarial de la Universidad de Costa Rica, ya que esta investigación fue parte de un proyecto final de graduación.
Publicado originalmente en e-Agronegocios Instituto Tecnológico de Costa Rica, Costa Rica ISSN-e: 2215-3462 Periodicidad: Semestral vol. 8, núm. 1, 25-44, 2022